ЖИВА МАТЕМАТИКА

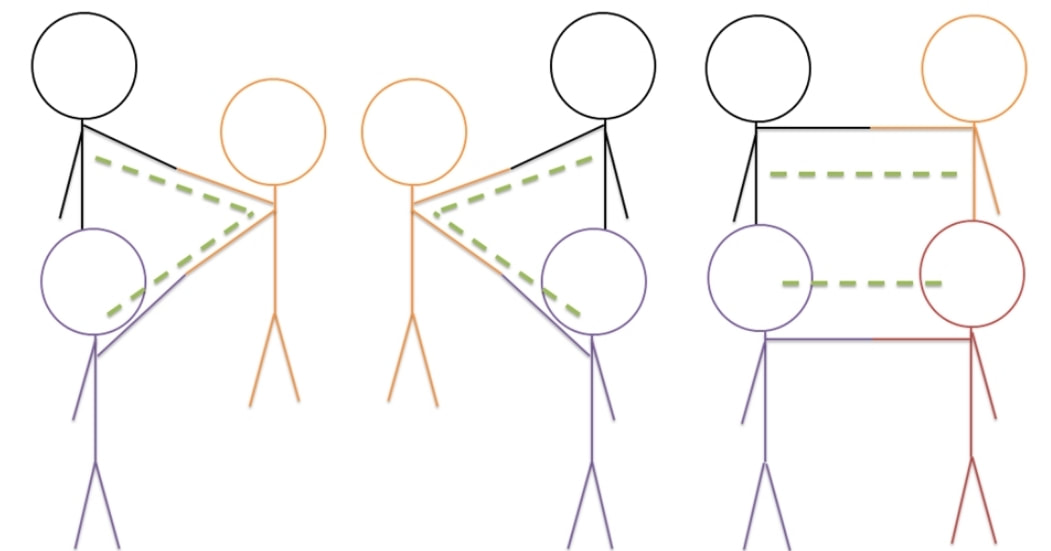
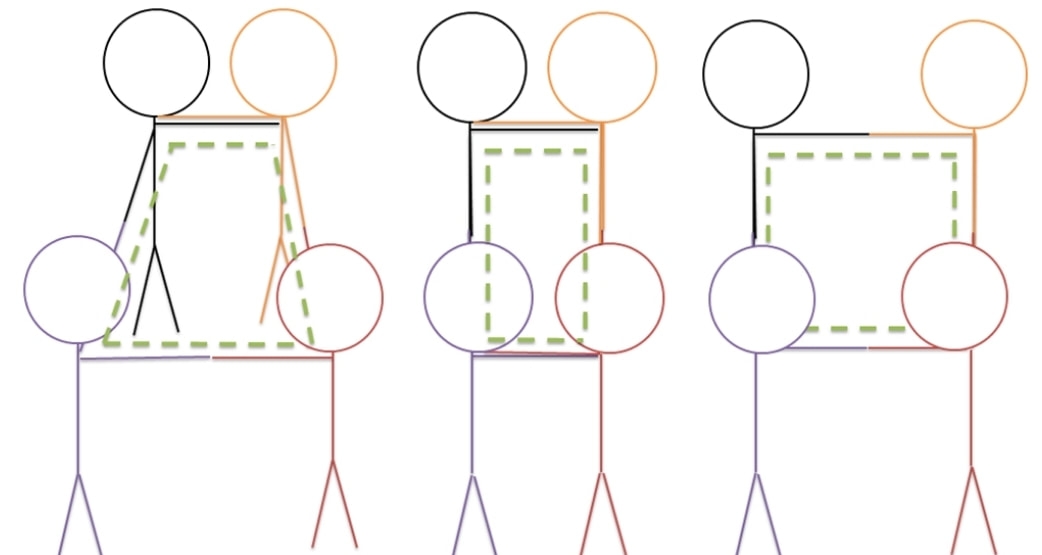
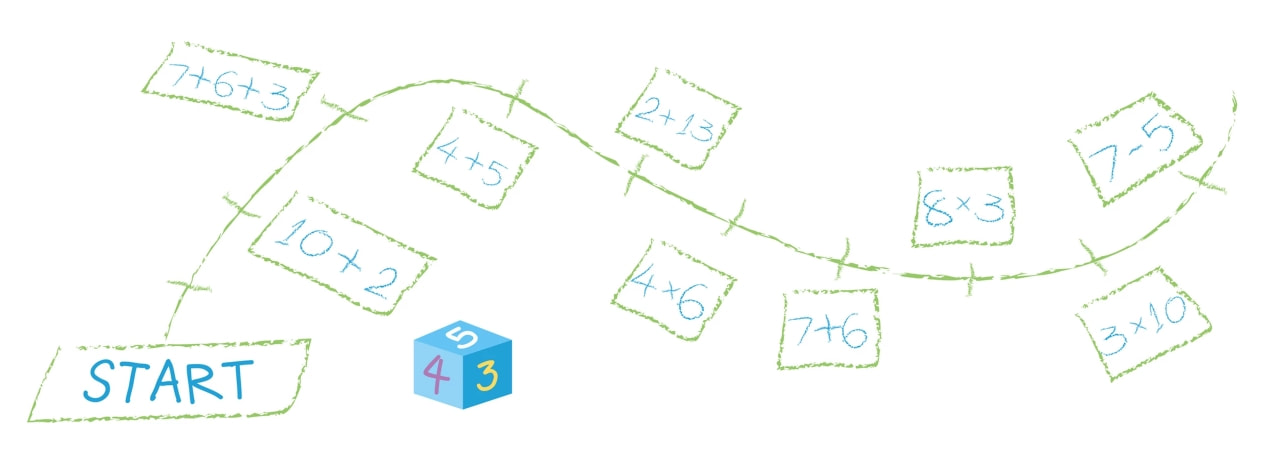
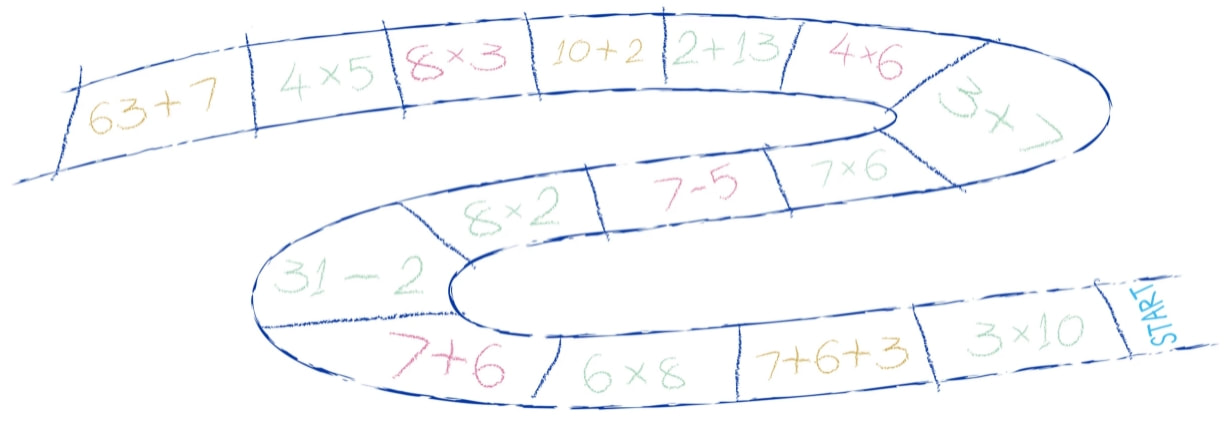
Интерактивните игри са задължителен елемент от живото учене. С тях лесно, интересно и изключително развиващо може да реализираме учене с разбиране. Математическите концепции за някои деца са самоподразбиращи се, но за други е нужно ангажиране на всички сетива, за да ги видят и усетят. Интеракцията осигурява усещане и възприемане чрез преживяване – тази формула ни дава трайност на понятието (защото изживяната емоция, както и направените познавателни изводи, се помнят най-дълго), както и мобилност (защото в хода на живите игри се създават условия за вариативност, за проверка на възможности, за грешка и поправяне, а това са ценни инструменти по пътя на осмислянето и осъзнаването чрез преживяване). Обиграването на математическата концепция я прави не просто добре усвоено понятие, то я превръща в ценно вътрешно усещане за откритие, за съучастие в процес на откривателство заедно с другите (т.е. създава умения за взаимодействие и учене в група, за екипност).

Идеи за живи математически игри
1. Живи знаци
Знаците >, < и = могат да се представят визуално и от самите деца (вж. схемите). Първоначално учителят извиква три деца пожелание за участие в игрова загадка. Той им дава словесни инструкции как да застанат. После се обръща към класа и пита (като показва полученото очертание на знака от заловените ръце на децата: Какъв знак нарисуваха тримата? (прим. >) Да докажем, че наистина е по-голямо. Отляво колко деца има? (2) А отдясно? (1) 2 по-голямо ли е от 1? (да) Следователно, този знак наистина е „по-голямо“. (При равно имаме 2:2. Децата отляво и отдясно са поравно.)
После учителят групира деца по 3-ки, за да образуват знак. След овладяването на всеки от знаците, учителят групира децата, като им възлага да образуват различни знаци (на една група знак по-голямо, на друга – по-малко и т.н. Пита ги за знак = колко деца са нужни и защо... Играта допуска многовариантност и извличане на различни изводи. ​

​2. Живи геометрични фигури
Живи геометрични фигури се образуват аналогично на знаците. За начало може да тръгнете от знак < или >, като накарате децата, които не са се заловили за ръце, да го направят. Така получавате триъгълник. Аналогично, за квадрат може да тръгнете от знак =. После от квадрата лесно се образува правоъгълник, като накарате децата да се захванат за раменете, образувайки срещуположни къси страни (вж. схемата). За 5-ъгълник питате: Четириъгълниците от колко деца се образуват? Колко деца ще са нужни, за да образуваме петоъгълник (респ. всякакъв др. правилен многоъгълник)? За неправилните може да използвате поставяне на ръце върху раменете на съотв. две съседни деца.

3. Живи числа
Правите кръгове и ги обозначавате с цифри. Избирате навигатор/разпределител на децата по кръгове (толкова деца в кръг, колкото показва цифрата,-ите) - І етап, а за ІІ етап децата сами се навигират, може да изберете само дете/деца за проверка на верността на изпълнение (групиране).
Тази игра може да се играе и с по-големи числа, като 1 дете = десетица, стотица, хиляда и т.н.
Може един кръг да бъде обозначен с число, което съдържа единици, десетици, стотици и пр. Ще са нужни съответно деца с такива стойности (обозначение с бадж/табелка). Тогава децата ще трябва да съобразят съответната цифрова позиция и нейната стойност в числото.

4. Живи математически редици
Децата са с баджове/табелки с определена цифра,-и. Първоначално учителят подрежда някои деца от редицата, като оставя няколко празни места със задачата да бъдат запълнени. После децата сами се организират за оформяне на цялата редица. Може да се образуват редици в прав и обратен ред, четни и нечетни числа и пр. Играе се и с големи числа (всичко зависи от надписите на баджовете).

5. Живи задачи
Тази игра има нужда от сценарист, който да запълва изходните правоъгълници за конкретната задача, и режисьор – това ще е детето, което ще реши задачата. Чертаете на земята три правоъгълника, между които поставяте знак + или – (между първите два) и = между втория и третия (вж. схемата). После обозначавате правоъгълниците с цифрите на съответните числа за задачата, която искате да решите.

​Сценаристът организира задаването на живата задача, като разпределя децата за първите два правоъгълника, а режисьорът после ги организира да застанат в третия така, че да му е лесно да пресметне и обяви резултата (по 2-ки, по 5-ци, по 10-ци и т.н.). Тук отново баджът е този, който определя едно дете каква числова стойност преставлява.
При задачи с изваждане, режисьорът може да сдвои деца (от първия и втория правоъгълник), като сдвоените (групираните по двойки) си сядат, а в третия правоъгълник остават излишните (тези, за които няма партньор). Разбира се, може да постъпи и по друг начин – оставяме това на изобретателността на децата.
При задачи с умножение (с едноцифрено число), децата от единия множител извикват толкова деца от класа, колкото показва другия множител (като броят и себе си в това число). Ако множителите са по-големи, може да поставите съответни баджове на деца. Например, ако искате да пресметнете 5.9, 5-те деца (на които също се поставя 9-ка) ще извикат 4 деца от класа с надпис 9 (може и с 9 квадратчета в един ред – за начало). Събраните общо 5 деца с надпис 9 се подреждат 1 до друго в последния правоъгълник. Питате: Числото 99999 ли е отговорът? (Не, нужно е тези 9-ки да се сумират и се получава......). Тази ситуация може да се отиграе много интересно и увлекателно, защото се получава задача с продължение (9+9+9....). Нека сценаристът и режисьорът доразвият постановката J по свое усмотрение.
При деление, първо се подрежда голямото число (делимото), после делителя, а частното се получава, като режисьорът прецени кои деца да седнат и кои да останат, мотивирайки се пред всички защо го прави. Може да се стимулира оригиналност в подхода (така децата сами дават оригинални решения за конкретна задача). При по-големи числа изобретателността на режисьора е ключова, като учителят определя какво може и какво не може да си позволи да прави и защо (задава правила) – прим. да извиква деца от публиката, да сменя бадж и т.н. Важното е не само да реши вярно задачата, а със средствата на театъра убедително визуално да демонстрира/обясни решението на задачата.

6. Жив часовник
Тази игра е любима на децата, които за първи път се запознават с часовника. Начертавате на пода циферблат (без стрелки, с обозначени часове). Поставяте баджове на децата, които ще участват (часовете от 1 до 12). Децата, които искат да са стрелки, също обозначавате по сътоветен начин. Децата часове по даден от вас знак си заемат местата и клякат. После назовавате час. Децата стрелки лягат по съответен начин, за да покажат този час. Питате: Вярно ли показват стрелките? Децата, които са на съответното място в часовете (и минутите) стават, за да покажат вярното решение (напр. за 2 и 20 стават децата на часове 2 и 4).
Друг вариант: задавате инструкция на стрелките къде да застанат, след което питате децата от публиката, колко е часът. Ако отговорът е верен, децата от циферблата (на сътоветните часове) стават прави.
Варианти за игра и тук има много...

7. Скачане по числова ос
"Скачането" по числова ос е един добре познат от нашите образователни ресурси начин за овладяване на четни-нечетни числа, десетици, стотици и т.н., математическите операции събиране и изваждане, въвеждане в концепциите за умножение и деление на числа. Предоставили сме ви много варианти на числови оси за копиране, ламиниране и "скачане". В живите задачи, обаче, децата скачат наистина.

Числовата ос може да се номерира според нуждите ни - с цифрите на числата от 0 до 10, от 10 до 100 по десетици, по петици и т.н. Важно е децата да разберат в кои случаи скачат напред и в кои назад и защо.
Може да използвате зарче, с което да се определи реда на скачане (от 1 до 6 - за 6 деца - по реда на числата, може и обратно). Със зарче може да скачате и за упражняване на таблицата за умножение. Например, детето хвърля 6 и скача, като всеки път назовава произведението (0.6=0, 1.6=6, 2.6=12 и т.н.)

7. Скачане по математическа пътечка

Начертайте числова ос с 12 деления. Тук може да използвате 1 или 2 зарчета (за числата от 7 до 12). С две зарчета децата събират получените числа, за да разберат колко пъти да скочат. Всеки път, когато се реши задачата, триете (може и някое дете да поеме ролята на Магистър - то да съставя нови задачи) и сменяте стойностите, без да сменяте знаците.
По тази числова пътека може да се скача и за време (бързина на решаване на задачите).

​8. Скачане в кръгове (таблица за умножение/деление до 10, с произведения/частни до 12)

Чертаете тези кръгове с тебешир, като оставяте празен (без цифри) или външния бял кръг - когато ще отигравате умножение, или синия кръг - за попълване при неизвестен множител или упражняване на деление. Определяте реда на действие, като предварително си подготвяте картончета с номера от 1 до 12. Обръщате ги с гръб към децата и всяко от тях си изтегля по една карта - тя показва задачата с кое число да реши (карти от 1 до 12) или кръга, по който да скача (карти от 1 до 10). После сменяте или редувате. Може децата сами да предложат система за редуване.
Тази игра е добре да я имате и в преснет и ламиниран вариант (таблички). Така децата ще могат да отиграват и с флумастри върху табличките. Eто и таблиците с по два вида кръгове - за попълване на произведения и с неизвестен множител - за различни игри): Times Tables to 10 Таблица за умножение до 10

Приятна и вълнуваща игра!